MathModDB
Proper documentation and storage of research data, adhering to FAIR principles, are crucial for reproducibility and scientific integrity. Applied mathematics, producing diverse numerical and symbolic data, heavily relies on models that must be well-documented for replication and future use. Here, we present MathModDB, an ontology for mathematical models, along with a knowledge graph containing. The work is conducted within the NFDI project entitled Mathematical Research Data Initiative (MaRDI).
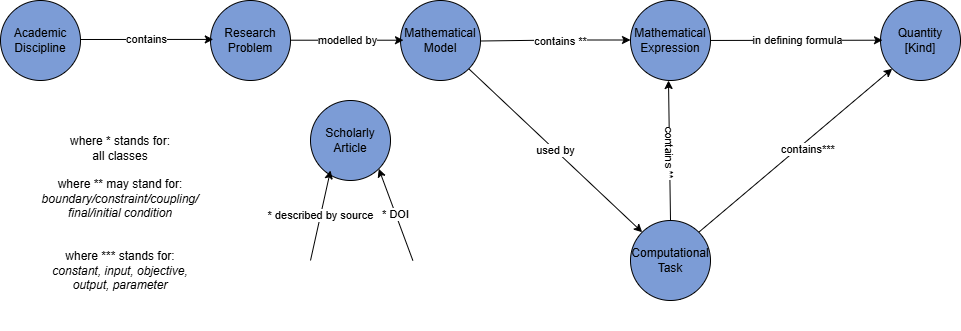
MathModDB is a database of mathematical models developed by MaRDIs TA4 as a knowledge graph). MathModDB defines a data model with classes (Mathematical Model, Mathematical Formulation, Research Field, Research Problem, Quantity [Kind], Computational Task, Publication), object properties/relations, data properties and annotation properties as an ontology. This ontology is populated with individuals/data from various fields of applied mathematics, making it a knowledge graph.
The ontology consists of the classes Mathematical Model, Mathematical Formulation, Computational Task, Quantity [Kind], Research Field and Research Problem. The structure of the ontology, in conjunction with the neighboring knowledge graph for mathematical algorithms MathAlgoDB is displayed in the image below:
Next, we show the total number of individuals per class and a detailed list of the individuals, when you click on the respective total number of individuals.
| Research Fields: 1 |
| Research Problems: 1 |
| Mathematical Models: 1 |
| Computational Tasks: 1 |
| Mathematical Expressions: 1 |
| Quantities: 1 |
| Quantity Kinds: 1 |
Publications
Following publications with respect to MathModDB have been published:
2024
Schembera, Björn, Frank Wübbeling, Hendrik Kleikamp, Burkhard Schmidt, Aurela Shehu, Marco Reidelbach, Christine Biedinger et al. "Towards a Knowledge Graph for Models and Algorithms in Applied Mathematics." In: Sfakakis, M., Garoufallou, E., Damigos, M., Salaba, A., Papatheodorou, C. (eds) Metadata and Semantic Research. MTSR 2024. Communications in Computer and Information Science, vol 2331. Springer, Cham. https://doi.org/10.1007/978-3-031-81974-2_8
2023
Schembera, B., Wübbeling, F., Kleikamp, H., Biedinger, C., Fiedler, J., Reidelbach, M., Shehu, A., Schmidt, B., Koprucki, T., Iglezakis, D. and Göddeke, D., 2023. Ontologies for Models and Algorithms in Applied Mathematics and Related Disciplines. arXiv preprint arXiv:2310.20443.
Schembera, B., Riethmüller, C. and Göddeke, D., Enabling FAIR Data in Computational Science, Engineering and Mathematics through Knowledge Graphs.
Schembera, B., Wübbeling, F., Koprucki, T., Biedinger, C., Reidelbach, M., Schmidt, B., Göddeke, D. and Fiedler, J., 2023, September. Building Ontologies and Knowledge Graphs for Mathematics and its Applications. In Proceedings of the Conference on Research Data Infrastructure (Vol. 1). https://doi.org/10.52825/cordi.v1i.255